Introduction
The ability to solve problems in a variety of contexts is an essential skill for all citizens of a modern society and is a major goal of education. Problem-solving skills are particularly important to scientists and engineers and because introductory physics is a gateway course for study in nearly all science, technology, engineering, and mathematics (STEM) fields at the postsecondary level, it is an ideal venue for teaching problem solving. However, although most introductory physics courses have the appearance of emphasizing problem solving, studies have shown that the majority of their students make little progress towards developing good problem-solving skills (Reif, 1995).
Researchers have shown that it is possible, through targeted efforts, to improve students’ problem-solving skills (see Maloney (1994) and Hsu, Brewe, Foster & Harper (2004) for overviews). The common thread running through these efforts is that they are all explicitly or implicitly based on the cognitive apprenticeship model (Collins, Brown & Newman, 1989). Two key features of this approach are that the cognitive processes necessary for solving problems are made explicit and that students practice using those processes to solve problems while receiving guidance and feedback. In contrast, traditional forms of instruction are less explicit about the strategic problem-solving process and do not include explicit coaching, instead focusing on tactics for a specific type of problem. One significant difficulty with implementing coaching however is that the opportunities for students to be coached are, at best, limited. Under such conditions, the advantages of any carefully designed curricula are diluted or can even be lost.
One possible solution to providing students with effective coaching lies in the creation of computer coaches, programs that can provide students with individualized guidance and feedback at the students’ convenience. Besides being available at all hours, computer coaches have a number of advantages, including infinite patience and being perceived as less judgmental than a human tutor. They are economical to operate and cost very little to maintain. Finally, computer coaches provide reproducible instruction that can be improved incrementally.
The coaches we envision and have been developing go far beyond the many web-based homework systems available for introductory physics that either check only the correctness of a student’s answer and offer very limited feedback, do not emphasize or coach the general decision-making processes involved in all problem solving, or are not easily adaptable by individual instructors to their own preferences. Although the task of creating an effective computer coach that can help students acquire better thinking skills is a difficult one (as evidenced by the fact that such coaches are not already a common component of education), we believe that using computers in this way has the potential to dramatically transform the nature of education.
Theoretical framework
The overall theoretical framework of these coaches is Cognitive Apprenticeship (Collins, Brown & Newman, 1989). Although human learning is complex and individual-specific, one type of pedagogy, apprenticeship, has been extremely successful for human learning throughout history and across cultures. Cognitive Apprenticeship analyzes the pedagogy of apprenticeship and applies that pedagogy to the intellectual processes usually taught in a classroom. Within this theory, the necessary functions of teaching include the actions of modeling, coaching, and fading, supported by temporary instructional tools called scaffolding. Essentially, modeling is showing students precisely what you want them to do by making all the intellectual processes visible. Coaching is giving students real-time feedback as they attempt the task by following the model in their own way. Fading is giving students the opportunity to do the task themselves without guidance or real time feedback. Scaffolding is temporary supports, or “training wheels,” that are removed as students become more proficient. All of these actions must take place in what is called the environment of expert practice where tasks include a meaningful context that have a meaningful outcome.
Teaching problem solving via a cognitive apprenticeship requires that the instructor model an organized problem-solving process that can be understood by the student, taking care to make the invisible thought processes involved visible and explicit. Interspersed with the modeling, the students need to be coached by being given guidance and feedback based on their own inclinations as they practice solving problems. The amount and focus of the coaching changes as the students become more competent at solving problems. Scaffolding such as the use of a specific problem-solving framework and problems designed to encourage expert-like behavior are introduced and removed throughout the process.
Computer coaches
The computer coaches are designed to emulate the behavior of expert teachers, incorporating the Cognitive Apprenticeship modalities of modeling, coaching, and fading. In particular, the computer coaches rely on the instructional strategies of reciprocal teaching (Palincsar & Brown, 1984) and learning from well-studied examples (Zhu & Simon, 1987). Reciprocal teaching is an instructional method consistent with Cognitive Apprenticeship in which students and teachers take turns playing the role of the teacher. To accomplish this we use two types of coaches which employ extensive scaffolding. A third type of coach emphasizes the fading part of the Cognitive Apprenticeship paradigm. Examples of the coaches can be found at http://groups.physics.umn.edu/physed/pscoaches.html.
In a type 1 coach, “Computer coaches student,” the computer models an organized decision framework for physics problem solving, making the numerous automated decisions of an expert visible. The student is asked to make those decisions and the computer assesses each decision as it is made. This feedback helps the student diagnose any errors and guides them to make any necessary corrections before moving on to the next decision in the process.

Fig. 1. Screenshot from a type 1 module (computer coaches student). The display shows a partially completed picture (1). The computer has decided on a step (2) and asks the student to specify the direction of a force (3). The student’s decision on this step (4) is incorrect, and the computer provides feedback (5). A red number to the right of each step (6) indicates the number of incorrect responses the student made during the implementation of that step, while a checkmark indicates that the step was implemented correctly the first time.
In a type 2 coach, “Student coaches computer,” the roles are reversed. The student chooses the decisions to be made, assesses the computer’s decisions, and makes any necessary corrections. Because some of the computer responses are designed to reflect incorrect student behavior, this coach also gives students practice in the important problem solving process of debugging. In this coach, the computer also acts in an oversight mode, assessing and giving feedback to the student’s responses.
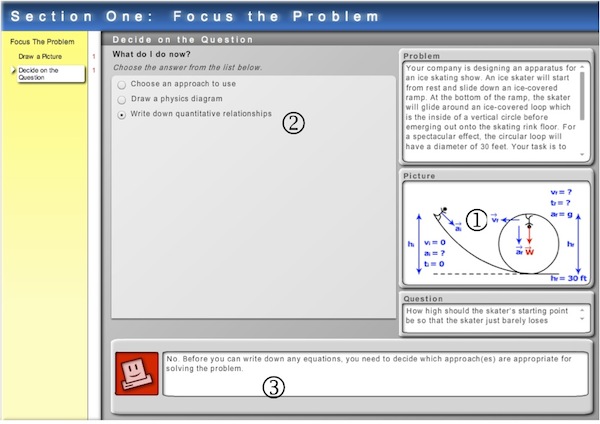
Fig. 2. Screenshot from a type 2 module (student coaches computer). The display shows a completed picture (1). The student, acting as a coach, has decided on a step for the computer, in its role as a student, to do (2), but it is not an appropriate step at this point. The computer, in its oversight role, gives the student feedback (3).
In the type 3 coaches, “Student works independently, computer gives feedback,” the computer presents a problem to the student, who is asked to solve the problem on paper, without any help. After the student enters an answer, the computer asks follow-up questions to verify the correctness of the student’s solution process, gives appropriate feedback, and if necessary, gives the student appropriate coaching. A student who cannot reach a solution on his or her own can ask for help. The coach helps the student to determine the point of difficulty and gives targeted coaching before the student resumes solving the problem.
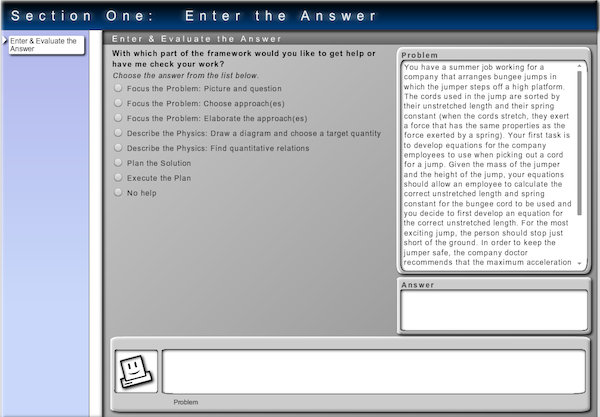
Fig. 3 Screenshot from a type 3 module (student works independently, computer gives feedback). If the student gets stuck solving a problem or enters an incorrect answer, the computer asks the student to decide where in the problem solving process the difficulty might occur.
The physics problems addressed by the coaches help establish the environment of expert practice in the Cognitive Apprenticeship pedagogy. These problems place the student into a situation which is concrete enough for them to imagine and gives the motivation for desiring a solution. In addition, they are designed to encourage expert-like behavior. This type of problem, known as a Context-rich problem, was developed by our research program to aid students in learning both physics and problem solving (Heller & Hollabaugh, 1992). They are currently used in physics and other disciplines as disparate as oral biology and economics. Each of the computer coaches at our website features a Context-rich problem.
Current work
We are presently developing the coaches through a continuous cycle of testing, assessment, and revision. The testing is being performed in the introductory physics classes at the University of Minnesota, both on the Twin Cities and Rochester campuses, and we hope to soon include some Minnesota high school physics classes. Assessment of the coaches’ educational impact is performed through an examination of the problem solutions that students produce on in-class exams, as well as standard assessments of students’ conceptual physics knowledge, mathematical skills, and attitudes and beliefs about physics.
Because the ability of individual instructors to adapt an educational tool to their own preferences and local conditions is critical to its use, we are also developing a graphical interface that allows typical physics teachers, without any programming experience, to modify the computer coaches themselves, generating new problems and problem types, new supports for their students, and new coaching methods that align with their own curricular preferences.
Potential impact and vision
Because problem solving is central to STEM courses, the coaches have the potential not only to become widely used, but also to spawn similar efforts in other STEM fields, and across multiple disciplines. Our work demonstrates how technology can be used to improve education by providing students with (1) more interactive and individualized instruction based on research from education and cognitive psychology, as well as from a STEM content area, (2) opportunities to integrate effective instruction outside with that occurring in the classroom, and (3) access to alternative forms of instruction, and we hope that it will provide a foundation for others on which to build and to improve. While not replacing human instruction, computer coaches can be a cost effective supplement to our educational system. This can be especially important to students for whom standard instruction is insufficient, such as underprepared students or students underrepresented in science. Computer coaches may also be an essential element to an effective distance learning application.
References
Collins, A., Brown, J.S., & Newman, S.E. (1989). Cognitive apprenticeship: Teaching the crafts of reading, writing and mathematics. In: L. Resnick, (Ed.) Knowing, learning and instruction. Hillsdale, NJ: Lawrence Erlbaum.
Heller, P. & Hollabaugh, M. (1992). Teaching problem solving through cooperative grouping. Part 2: Designing problems and structuring groups. American Journal of Physics, 60, 637644.
Hsu, L., Brewe, E., Foster, T. M., & Harper, K. A. (2004). Resource letter RPS-1: Research in problem solving. American Journal of Physics, 72, 1147-1156.
Maloney, D. P. (1994). Research on problem solving: Physics. In D. L. Gabel (Ed.), Handbook of research on science teaching and learning (pp. 327-356). New York: Macmillan.
Palincsar, A. L. & Brown, A. L. (1984). Reciprocal teaching of comprehension-fostering and comprehension-monitoring activities. Cognition and Instruction, 1, 117-175.
Reif, F. (1995). Millikan Lecture 1994: Understanding and teaching important scientific thought processes, American Journal of Physics, 63, 17-32.
Zhu, X. & Simon, H. A. (1987). Learning mathematics from examples and by doing. Cognition and Instruction, 4, 137-166.



